MiVolumeCell Class Reference
[Cell]
 Defines an abstract cell of an unstructured volume mesh.
More...
Defines an abstract cell of an unstructured volume mesh.
More...
#include <MeshVizXLM/mesh/cell/MiVolumeCell.h>
Public Member Functions | |
| virtual size_t | getNumFacets () const =0 |
| virtual size_t | appendNodesIndexOfFacet (size_t facet, std::vector< size_t > &facetNodes) const =0 |
| virtual size_t | getSubTriangleNodesIndex (size_t facet, std::vector< size_t > &triangleNodeIds) const |
| virtual size_t | getSubTetrahedronNodesIndex (std::vector< size_t > &tetrahedronNodeIds) const |
| virtual size_t | appendLocalNodesIndexOfFacet (size_t facet, std::vector< size_t > &facetNodes) const |
| virtual void | getIsosurfTopology (unsigned char caseId, std::vector< std::pair< size_t, size_t > > &edgeList) const =0 |
| virtual unsigned char | getMarchingCaseId (std::vector< bool > &nodesSign, size_t beginNodeId=0) const |
| virtual MbVec3d | getFacetCenter (size_t facet, const MiGeometryI &geometry) const |
Protected Member Functions | |
| virtual std::ostream & | toStream (std::ostream &s) const |
Detailed Description
 Defines an abstract cell of an unstructured volume mesh.
Defines an abstract cell of an unstructured volume mesh.
A volume cell is a polyhedron element that connects adjacent nodes of a volume mesh.
This class defines additional methods beyond MiCell to gives a complete description of a volume cell.
- Definition of the facet numbering.
See getNumFacets(), appendNodesIndexOfFacet(), appendLocalNodesIndexOfFacet(). - Definition of the isosurface topology in this cell.
See getIsosurfTopology() and getMarchingCaseId(). - Definition of a sub triangulation for each facet of the cell.
See getSubTriangleNodesIndex(). - Definition of sub tetrahedra of the cell.
See getSubTetrahedronNodesIndex().
The methods getSubTriangleNodesIndex() and getSubTetrahedronNodesIndex() are only useful for non linear volume cells and generic polyhedron cells. For the most usual basic volume cells (tetrahedron, hexahedron, wedge, pyramid), the application only needs to implement facet numbering, the isosurface topology, and the methods defined in MiCell.
When the result of getSubTetrahedronNodesIndex() is > 0, the cell is considered to be a non linear cell, or a generic polyhedron cell. In that case, the given sub triangles and sub tetrahedra are used by various extractors (for instance MiSkinExtractUnstructured) and mesh representation classes (for instance MoMeshSkin, MoMeshCellShape). Furthermore if an MiTessellator is given, each sub triangle is tessellated by the method MiTessellator::tessellateSurfaceCell().
The utility classes MxXXXCellExtract can be used to help the application implement the various methods of MiCell and MiVolumeCell. These classes provide static implementations of the necessary methods for the most common linear and quadratic volume cells.
- See also:
- MeXVolumeCell
- MiVolumeTopologyExplicitI
- MiTessellator
- MxTetrahedronCellExtract
- MxHexahedronCellExtract, MxHexahedron20CellExtract, MxHexahedron27CellExtract
- MxWedgeCellExtract, MxWedge18CellExtract
- MxPyramidCellExtract
- See related examples:
Member Function Documentation
| virtual size_t MiVolumeCell::appendLocalNodesIndexOfFacet | ( | size_t | facet, | |
| std::vector< size_t > & | facetNodes | |||
| ) | const [inline, virtual] |
Appends the array of local node indices belonging to a given facet to facetNodes.
This method is similar to appendNodesIndexOfFacet() but facetNodes must be filled only with local node ids (i.e. node ids relative to the number of nodes in the cell): 0 <= facetNodes[i] < getNumNodes() for each i.
The method must not include the additional nodes of a non linear cell. For instance an implementation of this method for a linear or quadratic tetrahedron cell like the following one

facetNodes of the pink face of these tetrahedra.
should return 3, and facetNodes should be appended by {0,2,1} if the facet argument corresponds to the pink one. (Provided that getNodeIndex() follows this tetrahedron node numbering.)
- Parameters:
-
[in] facet The index of the facet (where 0 <= facet < getNumFacets()). facetNodes A vector in which the local node indices of the facet will be appended. The given vector should not be cleared by this method. The implementation must use the push_back() method to add elements to the vector.
- Returns:
- the number of nodes added.
| virtual size_t MiVolumeCell::appendNodesIndexOfFacet | ( | size_t | facet, | |
| std::vector< size_t > & | facetNodes | |||
| ) | const [pure virtual] |
Appends the array of node indices belonging to a given facet to facetNode.
The method must not include the additional nodes of the non linear cell. For instance an implementation of this method for a linear or quadratic tetrahedron cell like the following one

facetNodes of the pink face of these tetrahedra.
should return 3, and facetNodes should be appended by = {node0,node2,node1} if the facet argument corresponds to the pink one. (Provided that getNodeIndex() follows this tetrahedron node numbering.)
- Parameters:
-
[in] facet The index of the facet (where 0 <= facet < getNumFacets()). facetNodes A vector in which the node indices of the facet will be appended. The given vector should not be cleared by this method. The implementation must use the push_back() method to add elements to the vector.
- Returns:
- the number of nodes appended in facetNodes.
| MbVec3d MiVolumeCell::getFacetCenter | ( | size_t | facet, | |
| const MiGeometryI & | geometry | |||
| ) | const [inline, virtual] |
Gets the center of the specified cell facet.
This method is not pure virtual because it is not used by all extraction classes. The default implementation provided computes the average of the coordinates of each facet's node.
- Parameters:
-
[in] facet a facet id of this cell. It must be < getNumFacets(). [in] geometry The geometry of the mesh. Used to retrieve the node coordinates of this cell.
- Returns:
- The center of the specified facet.
| virtual void MiVolumeCell::getIsosurfTopology | ( | unsigned char | caseId, | |
| std::vector< std::pair< size_t, size_t > > & | edgeList | |||
| ) | const [pure virtual] |
Gets the list of topological polygons defining the part of the isosurface topology in this cell.
This method is used during isosurface and slice extraction on an unstructured mesh (for instance MoMeshPlaneSlice, MoMeshIsosurface, MiIsosurfExtractUnstructured). Static implementations are provided for the most common basic volume cells:
- See MxHexahedronCellExtract::getIsosurfTopology()
- See MxTetrahedronCellExtract::getIsosurfTopology()
- See MxWedgeCellExtract::getIsosurfTopology()
- See MxPyramidCellExtract::getIsosurfTopology()
For polyhedral cells and non linear cells (for which no static implementation is available), returning an empty list can produce a hole in the isosurface. To avoid such a hole, this kind of cell must provide a decomposition into sub tetrahedra by the method getSubTetrahedronNodesIndex(). In case of polyhedral cells, one can also simply provide a polyhedral tessellator (
- See also:
- MiTessellator::getNewTessellatorPolyhedron()) to the isosurface extractor. To summarize:
- For basic cell shape (hexahedron, tetrahedron, wedge, pyramid), implement this method for example by calling MxXXXXCellExtract::getIsosurfTopology() and do not override getSubTetrahedronNodesIndex().
- Otherwise, implement this method by giving an empty edgeList and either implement getSubTetrahedronNodesIndex() to provide a sub tetrahedra decomposition or for polyhedral cells only, provide a polyhedral tessellator to the isosurface extractor.
- Parameters:
-
caseId the isosurf "marching cube" entry for this cell. This is the value returned by getMarchingCaseId edgeList the list of pairs of nodes defining the isosurface topology in this cell. The given vector should not be cleared by this method. New pairs of node ids are appended to this vector. Each pair of nodes must correspond to an edge of the cell which is cut by the isosurface. An edge is cut by the isosurface when the two nodes of the edge have different signs. The pair of nodes must be correctly ordered to define a non manifold polygon. When the isosurface part is made up of several polygons, extra polygons must be separated by specific pairs (for instance <-1,-1> for mandatory polygons and <-1,0> for optional polygons).
| unsigned char MiVolumeCell::getMarchingCaseId | ( | std::vector< bool > & | nodesSign, | |
| size_t | beginNodeId = 0 | |||
| ) | const [inline, virtual] |
Gets the isosurface "marching cube" entry according to the sign of each node in the cell.
The return entry corresponds to the first argument of getIsosurfTopology(). This method is used during isosurface and slice extraction on an unstructured mesh (for instance MoMeshPlaneSlice, MoMeshIsosurface, MiIsosurfExtractUnstructured).
- Parameters:
-
nodesSign A vector containing as many booleans as the number of nodes in the mesh. nodesSign[i] is relative to the sign of the (isovalue-i-th node's value) . beginNodeId is the first node id used by the mesh topology.
- Returns:
- a binary word containing as many bits as the number of nodes in the cell. the i-th bit in the returned word equals nodesSign[getNodeIndex(i)].
- Note:
- MeshViz XLM assumes that the cell does not contain any part of an isosurf if and only if the "marching cube" entry equals 0. Thus if all the bits in this word are 1, the method returns 0.
| virtual size_t MiVolumeCell::getNumFacets | ( | ) | const [pure virtual] |
Gets the number of facets.
| virtual size_t MiVolumeCell::getSubTetrahedronNodesIndex | ( | std::vector< size_t > & | tetrahedronNodeIds | ) | const [inline, virtual] |
Get a decomposition in sub-tetrahedra of this volume cell.
This method must be overridden to correctly handle non-linear cells. By default it returns 0 and the argument tetrahedronNodeIds is not modified. This method must not be overridden for linear cells.
- Parameters:
-
[out] tetrahedronNodeIds sub tetrahedra node id (where: 0 <= tetrahedronNodeIds[i] < getNumNodes() for each i). If the cell is not linear, tetrahedronNodeIds must contain 4 times the number of sub-tetrahedra.
- Returns:
- the number of sub-tetrahedra in this cell. 0 by default.
| virtual size_t MiVolumeCell::getSubTriangleNodesIndex | ( | size_t | facet, | |
| std::vector< size_t > & | triangleNodeIds | |||
| ) | const [inline, virtual] |
Get a triangulation of the given facet of a non linear volume cell.
This method must be overridden to correctly handle non-linear cells. For instance an implementation of this method for a quadratic tetrahedron like the following one
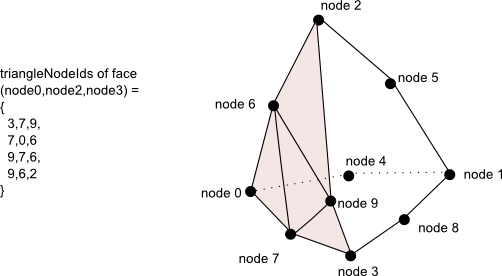
Triangulation of the pink face of this quadratic tetrahedron.
should return 4, and triangleNodeIds = {3,7,9, 7,0,6, 9,7,6, 9,6,2}. (provided that getNodeIndex() follows this tetrahedron node numbering).
By default the method returns 0 and the argument triangleNodeIds is not modified. It must not be overridden for linear cell.
- Parameters:
-
[in] facet number of the given facet. (where: 0 <= face < getNumFacets() ). [out] triangleNodeIds sub triangle node id (where: 0 <= triangleNodeIds[i] < getNumNodes() for each i).
- Returns:
- the number of sub triangles in the facet of the cell.
| std::ostream & MiVolumeCell::toStream | ( | std::ostream & | s | ) | const [inline, protected, virtual] |
Performs an output operation on a stream which is returned afterward. This method is protected since only called by the output operator <<. This method is not pure virtual and output by default the geometry and topology of a mesh. Whenever a different output is needed, this method can be implemented in the subclass to get a different output format. No std::ostream& operator << needs to be defined in any subclass. This allows you to benefit from the virtual inheritance when using the output operator on an abstract class.
Reimplemented from MiCell.
The documentation for this class was generated from the following file:
- MeshVizXLM/mesh/cell/MiVolumeCell.h