Computational Geometry
[Image Segmentation]

This group contains engines capable of transforming images into geometric objects. More...

Classes
class	SoCenterLineApproximation3d
	SoCenterLineApproximation3d engine More...
class	SoObjectToSegmentApproximation2d
	SoObjectToSegmentApproximation2d engine More...
class	SoPolylineExtrusionApproximation3d
	SoPolylineExtrusionApproximation3d polyline approximation. More...
class	SoPolylineResamplerApproximation2d
	SoPolylineResamplerApproximation2d polyline approximation. More...
class	SoPolylineResamplerApproximation3d
	SoPolylineResamplerApproximation3d polyline approximation. More...
class	SoQuadrilateralMeshSlicerApproximation3d
	SoQuadrilateralMeshSlicerApproximation3d engine More...
class	SoSurfaceFittingApproximation3d
	SoSurfaceFittingApproximation3d surface approximation. More...
class	SoSurfaceUnfoldingProcessing3d
	SoSurfaceUnfoldingProcessing3d engine More...

Detailed Description

This group contains engines capable of transforming images into geometric objects.

Introduction to segment objects

Contour chaining involves representing edge lines as a list of consecutive pixels. This change in the representation, called vectorization, is most suitable for binary lines of one pixel thickness resulting from the SoZeroCrossingsProcessing2d or SoGradientLocalMaximaProcessing2d commands.

Although many applications do not require vectorized edges, it results in a vast reduction of data, and it provides a representation more suitable for some algorithms. In particular, it is possible to process chains with computational geometry algorithms or 1D signal processing operators, and to solve problems that have a better formulation within these theories.

A chain consists of a list of adjacent pixels of an edge lying between two free ends, two triple points, or a free end and a triple point, as represented in Figure 1. Chains are oriented, and the orientation may be a function of the gradient. Each chain has a header containing information such as the size, the numbers of the previous or next connected chains, etc..

Figure 1: Chains representation

It makes data far less dependent on the digitization to approximate these chains as polygons composed of linear segments, as in Figure 2. This results in another reduction of data. A compression ratio of 1:50 from the original data is common. It is then possible to perform computations that would be otherwise very long.

Figure 2: Polygonal approximation with different value of angle

There are many algorithms to find polygonal approximations of chains. We shall outline a polygonal approximation scheme based on cone covering.

Let 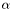$\alpha$ be an angle and 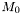$M_0$ the first point of the chain:

1. For each point 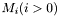$M_i (i>0)$ , a cone 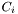$C_i$ of summit 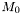$M_0$ , of axis 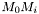$M_0M_i$ and of angle 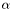$\alpha$ can be defined;

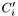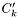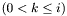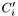2. Let $C'_i$ be the intersection of the $C'_k$ 's $(0<k\le i)$ : if $C'_i$ is not empty, starting from 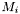$M_i$ , one can search for 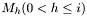$M_h (0<h\le i)$ , the first point for which the distance to the axis of 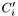$C'_i$ is a local minimum. The point 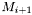$M_{i+1}$ is then examined (back to 1).

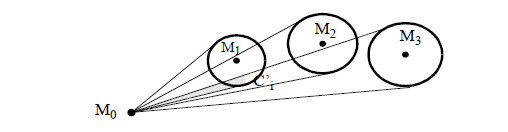
Figure 3: Polygonal approximation based on the cone covering

3. If 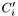$C'_i$ is empty, the last point 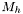$M_h$ is retained as the end of the segment. 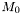$M_0$ is then replaced by 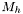$M_h$ and the next end can be determined.

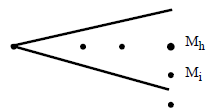
Figure 4: Chain definition

The parameter 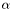$\alpha$ can be interpreted as a scale factor. A small angle picks up short ranged variations in curvature and yields many segments. A large angle produces few segments but the resulting approximation is blind to local details. The choice of a relevant 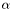$\alpha$ depends very much on the problem being studied.

Computational Geometry [Image Segmentation]

Classes

Detailed Description

Introduction to segment objects

Computational Geometry
[Image Segmentation]