SoAutoThresholdingQuantification Class Reference
[Statistics]
 SoAutoThresholdingQuantification engine
More...
SoAutoThresholdingQuantification engine
More...
#include <ImageViz/Engines/ImageAnalysis/Statistics/SoAutoThresholdingQuantification.h>
Classes | |
| class | SbAutoThresholdingDetail |
| Results details of threshold by automatic segmentation. More... | |
Public Types | |
| enum | RangeMode { MIN_MAX = 0, OTHER = 1 } |
| enum | ThresholdCriterion { ENTROPY = 0, FACTORISATION = 1, MOMENTS = 2 } |
Public Member Functions | |
| SoAutoThresholdingQuantification () | |
Public Attributes | |
| SoSFEnum | computeMode |
| SoSFImageDataAdapter | inGrayImage |
| SoSFEnum | rangeMode |
| SoSFVec2f | intensityRangeInput |
| SoSFEnum | thresholdCriterion |
| SoImageVizEngineAnalysisOutput < SbAutoThresholdingDetail > | outResult |
Detailed Description
 SoAutoThresholdingQuantification engine
SoAutoThresholdingQuantification engine
The SoAutoThresholdingQuantification engine extracts a value to automaticaly threshold on a gray level image.
Three methods of classification are available: Entropy, Factorisation or Moments. The computed threshold is provided in the SbAutoThresholdingDetail object.
Entropy
The entropy principle defines 2 classes in the image histogram by minimizing the total classes' entropy, for more theory the reader can refers to references [1] and [2]. Considering the first-order probability histogram of an image and assuming that all symbols in the flowing equation are statistically independent, its entropy (in the Shannon sense) is defined as:
![\[H=-\sum_{i=0}^{n} p[i] \times \log(p[i])_ 2\]](form_277.png)
Where 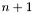 is the number of grayscales,
is the number of grayscales, ![$p[i]$](form_279.png) the probability of occurrence of level and
the probability of occurrence of level and 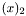 is the log in base 2.
is the log in base 2.
Let us denote 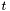 the value of the threshold and
the value of the threshold and ![$[I_1,I_2]$](form_282.png) the search interval. We can define two partial entropies:
the search interval. We can define two partial entropies:
![\[H_w[t]=-\sum_{I_1}^{t} p_1[i] \times \log(p_1[i])_2\]](form_283.png)
![\[H_b[t]=-\sum_{t+1}^{I_2} p_2[i] \times \log(p_2[i])_2\]](form_284.png)
Where ![$p_1[i]$](form_285.png) defines the probability of occurrence of level in the range
defines the probability of occurrence of level in the range ![$[I_1,t]$](form_286.png) and
and ![$p_2[i]$](form_287.png) defines the probability of occurrence of level
defines the probability of occurrence of level  in the range [t+1,I2]. We search the threshold value
in the range [t+1,I2]. We search the threshold value 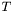 which minimizes the sum
which minimizes the sum ![$S(t)=H_w[t]+H_b[t]$](form_290.png) :
:
![\[T=\arg min_t(H_w[t]+H_b[t])\]](form_291.png)
| 
|
Factorization
The factorization method is based on the Otsu criterion (see [3] for details), i.e. minimizing the within-class variance:
![$\sigma^2_W[t]=w_0[t] \times \sigma_0^2[t]+w_1[t] \times \sigma_1^2[t]$](form_292.png)
Where ![$w_0[t]$](form_293.png) and
and ![$w_1[t]$](form_294.png) are respectively the probabilities occurrence
are respectively the probabilities occurrence ![$^2[t]$](form_295.png) and
and ![$^2[t]$](form_295.png) , the variances of classes
, the variances of classes  and
and 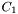 .
.
A faster and equivalent approach is to maximize the between-class variance:
![\[\sigma_B^2[t]=w_0[t] \times w_1[t] \times (\mu_0[t]-\mu_1[t])^2\]](form_298.png)
The within-class variance calculation is based on the second-order statistics (variances) while the between-class variance calculation is based on the first order statistics (means). It is therefore simplest and faster to use this last optimization criterion. We then search the value 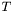 which maximizes the between-class variance such as:
which maximizes the between-class variance such as:
![\[T=\arg min_t(\sigma_B^2[t])\]](form_299.png)
| 
|
Moments
The moment SoAutoThresholdingProcessing uses the moment-preserving bi-level thresholding described by W.H.Tsai in [4]. Moments of an image can be computed from its histogram in the following way:
![\[m_j=\sum_{i=0}^n p[z_i]^j\]](form_300.png)
Where ![$p[z_i]$](form_301.png) is the probability of occurrence of grayscale
is the probability of occurrence of grayscale 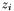 . For the following we note
. For the following we note 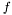 the original grayscale image and
the original grayscale image and 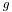 the threshold image. Image
the threshold image. Image 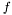 can be considered as a blurred version of an ideal bi-level image which consists of pixels with only two gray values:
can be considered as a blurred version of an ideal bi-level image which consists of pixels with only two gray values: 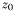 and
and 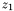 . The moment-preserving thresholding principle is to select a threshold value such that if all below-threshold gray values of the original image are replaced by
. The moment-preserving thresholding principle is to select a threshold value such that if all below-threshold gray values of the original image are replaced by 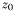 and all above threshold gray values replaced by
and all above threshold gray values replaced by 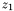 , then the first three moments of the original image are preserved in the resulting bi-level image. Image
, then the first three moments of the original image are preserved in the resulting bi-level image. Image 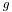 so obtained may be regarded as an ideal unblurred version of
so obtained may be regarded as an ideal unblurred version of 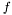 . Let
. Let 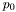 and
and 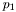 denote the fractions of the below-threshold pixels and the above-threshold pixels in
denote the fractions of the below-threshold pixels and the above-threshold pixels in 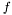 , respectively, then the first three moments of
, respectively, then the first three moments of 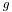 are:
are:
![\[m'_j=\sum_{i=0}^n p[z_i]^j\mbox{, j=0,1,2,3}\]](form_309.png)
And preserving the first three moments in 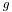 , means the equalities:
, means the equalities:
![\[m'_j=m_j\mbox{, j=0,1,2,3}\]](form_310.png)
To find the desired threshold value 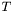 , we can first solve the four equations system to obtain
, we can first solve the four equations system to obtain 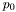 and
and 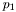 , and then choose
, and then choose 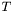 as the
as the 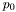 -tile of the histogram of
-tile of the histogram of 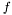 . Note that
. Note that 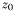 and
and 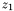 will also be obtained simultaneously as part of the solutions of system.
will also be obtained simultaneously as part of the solutions of system.
| 
|
[1] T.Pun, Entropic thresholding: A new approach, comput. Graphics Image Process. 16, 1981, 210-239
[2] J. N. Kapur, P. K. Sahoo, and A. K. C. Wong, "A New Method for Gray-Level Picture Thresholding Using the Entropy of the Histogram" Computer Vision, Graphics and Image Processing 29, pp. 273-285, Mar. 1985
[3] Otsu, N. 1979. A thresholding selection method from grayscale histogram. IEEE Transactions on Systems, Man, and Cybernetics9(1): 62-66
[4] Tsai, W. H. 1985. Moment-preserving thresholding: A New Approach. Computer Vision, Graphics, and Image Processing 29: 377-393
SEE ALSO
FILE FORMAT/DEFAULT
- AutoThresholdingQuantification {
| computeMode | MODE_AUTO |
| inGrayImage | NULL |
| rangeMode | MIN_MAX |
| intensityRangeInput | 0.0f 255.0f |
| thresholdCriterion | ENTROPY |
Library references: auto_threshold_value
Member Enumeration Documentation
- Enumerator:
MIN_MAX With this option the histogram is computed between the minimum and the maximum of the image.
OTHER With this option the histogram is computed between user-defined bounds intensityRangeInput.
- Enumerator:
Constructor & Destructor Documentation
| SoAutoThresholdingQuantification::SoAutoThresholdingQuantification | ( | ) |
Constructor.
Member Data Documentation
Select the compute Mode (2D or 3D or AUTO) Use enum ComputeMode.
Default is MODE_AUTO
The input grayscale image Default value is NULL.
Supported types include: grayscale image.
| SoImageVizEngineAnalysisOutput<SbAutoThresholdingDetail> SoAutoThresholdingQuantification::outResult |
The thresholding results.
Default value is NULL.
The input intensity range.
Use enum RangeMode. Default is MIN_MAX
The criterion to detect thresholds on histogram.
Use enum ThresholdCriterion. Default is ENTROPY
The documentation for this class was generated from the following file:
- ImageViz/Engines/ImageAnalysis/Statistics/SoAutoThresholdingQuantification.h