Image Filtering
[Engines]
This category gathers engines for filtering images. More...
Modules | |
| Color Transforms | |
| Frequency Domain | |
| Grayscale Transforms | |
| Sharpening | |
| Smoothing And Denoising | |
| Texture Filters | |
Detailed Description
This category gathers engines for filtering images.
Image Filters
- A filter transforms an image to emphasize or stress a specific feature of its structure. Filtering techniques are often useful to extract desired information from input data or simply to improve the appearance of the input data. For example, filtering techniques are used to remove noise from corrupted images or to enhance poorly contrasted or other images.
- Removing a grid consisting of uniformly spaced dark lines superimposed on an image.
- Restoring an image blurred by some degradation processes. (A difficult problem, the solution to which requires a very good knowledge of the degradation process itself.)
A common problem in filtering theory is to estimate a signal mixed with noise. A solution is the moving average , where the value of each pixel is replaced by the average of its neighbors (Figure 1). This is based on the assumption that short ranged variations result from noise. The filtered output can then be viewed as the main trend of the function.
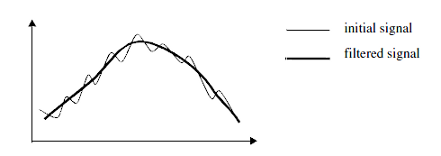
Figure 1: A moving average
Local changes in intensity present another common problem. Various filters can detect sharp transitions to enhance, contrast or detect edges. The Edge Detection algorithms use these types of filters.
Apart from the examples above, specific filters can be designed depending of the type of desired transition, such as:
From the mathematical point of view, a filter is an operator mapping an input function 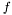 to an output function
to an output function 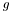 :
: 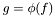 where
where 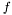 and
and 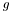 denote two functions of
denote two functions of 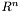 .
.
If 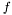 is an image
is an image 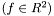 , the output function is the filtered image.
, the output function is the filtered image.
Linear and Non-linear Filters
- Filters are usually distinguished as linear or non-linear. Linear filters are widely used because they are easy to implement and, often, very intuitive. A filter
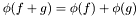
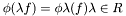
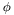 is linear if:
is linear if:
The class of non-linear filters is too large to be presented in a comprehensive way here. Besides, many non-linear filters are in fact particular algorithms that do not fall into a specific theoretical family. Non-linear filters include SoDelineateProcessing and SoShadeProcessing2d in the Sharpening category, as well as the SoMedianFilterProcessing in the Smoothing And Denoising category.
Some non-linear filters like the SoBitShiftProcessing filter are shift invariant filters, i.e. filters such that: ![$\phi(f_h) = [\phi(f)]_h$](form_414.png) where
where 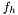 denotes the function
denotes the function 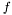 translated by vector
translated by vector 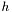 .
.
Shift invariant filters have the same effect on 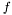 and its translated representations, which means that it is based on neighborhood operators where the same operations are performed around each pixel of the image.
and its translated representations, which means that it is based on neighborhood operators where the same operations are performed around each pixel of the image.