Edge Marking
[Edge Detection]
Introduction to Edge Marking
-
More...
Detailed Description
Introduction to Edge Marking
With gradient (ex: SoGradientOperatorProcessing2d) or laplacian (ex: SoRecursiveLaplacianProcessing) engines, a 1D edge was defined as the local maximum of the magnitude of the first derivative, or the zero crossing of the second derivative. Unfortunately, this definition cannot be extended to 2D functions (like for instance SoGradientLocalMaximaProcessing2d). In fact, an edge appears like a crest line on the magnitude of the gradient image and this leads us to define an edge as all the points whose gradient magnitude is maximum along the direction of the gradient, i.e the direction across the edge. This method, referred to as non-maxima suppression, provides thin lines which are much more convenient to handle.
Note that images of zero crossings of the Laplacian result in closed thin lines as they correspond to boundaries between positive and negative regions. Finally, we can take into account the specific geometry of a contour - its pixels are connected by using a more sophisticated threshold, the threshold by hysteresis (SoHysteresisThresholdingProcessing).
This is in fact an intuitive method. We choose a high and low threshold,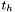 
and 
, and 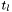decide that all the pixels with intensity higher than 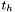are edges and those with are edges and those with intensity less than 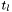are noise. For the transition area 
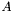, i.e. pixels with intensity lies between 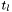and 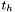, we only retain the pixels connected by a line included in 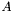to a pixel with a high intensity.
Figure1: Gradient image
Figure2: Threshold
Figure3: Threshold by hysteresis